Merkle Tree in Solana

What is Merkle Tree

Note: 这里仅讨论 Solana 中的 Merkle Tree (以具体实现为准)，在实际应用中不同链的 Merkle Tree 的一些细节处理可能存在差异。

Definition

默克尔树 (Merkle Tree) 是一种二叉树，其所有节点的 value为一个哈希值，为其左右儿子哈希值的 Hash 运算。 形式化定义 Solana 里的并发默克尔树，使用 $D$ (Depth) 来表示树的深度：

1. Merkle Tree 是一棵满二叉树
2. Node Index $X_i$ 范围 $1$ 到 $2^{D+1}-1$
3. 对于所有 $i<2^D$，满足节点 $X_i=H(X_{2i},X_{2i+1})$，即非叶节点的值为其左右子节点的哈希值
4. 叶子节点 ($i\ge 2^D$)，其值为 fingerprinted data
5. Leaf Index 范围 $0$ 到 $2^D-1$，若其 Node Index 为 i，那么可以算出 Leaf Index: $i-2^D$
6. 定义 rightmost leaf 为从左到右第一个空的叶子节点
7. 每个节点上的值为 256 bit

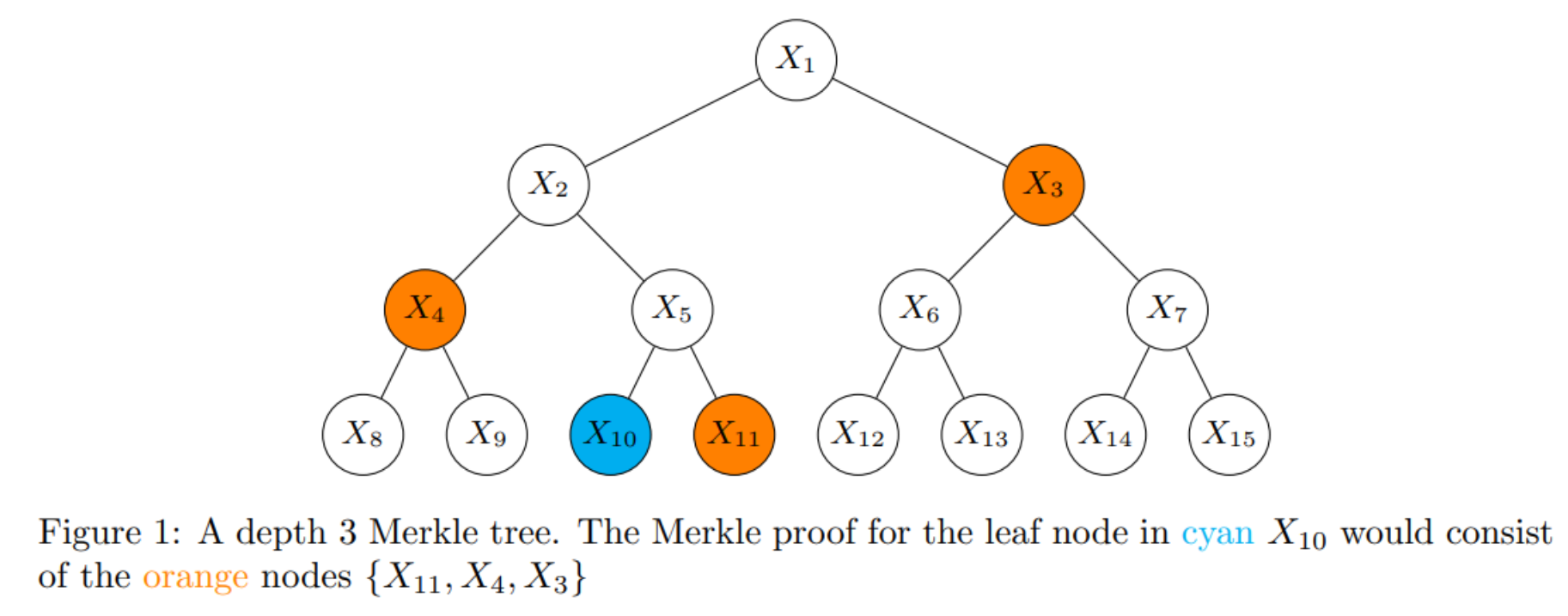
上图例子是深度为 3 的默克尔树。

Leaf Proof

想要证明某一叶子节点 $X_i$ 在以 $X_1$ 为 root 的 Merkle Tree 上，只需要提供一组 Proof，依次进行 hash 操作，然后比较 Merkle root 是否一致，一颗具有 n 个叶子节点的树证明所需的节点个数为 ${\log }_{2}n$ 即为深度$D$。 以前面图中的 $X_{10}$ 为例，那么需要提供的 Proof 为 $\{X_{11},X_4,X_3\}$。

Concurrency Problem

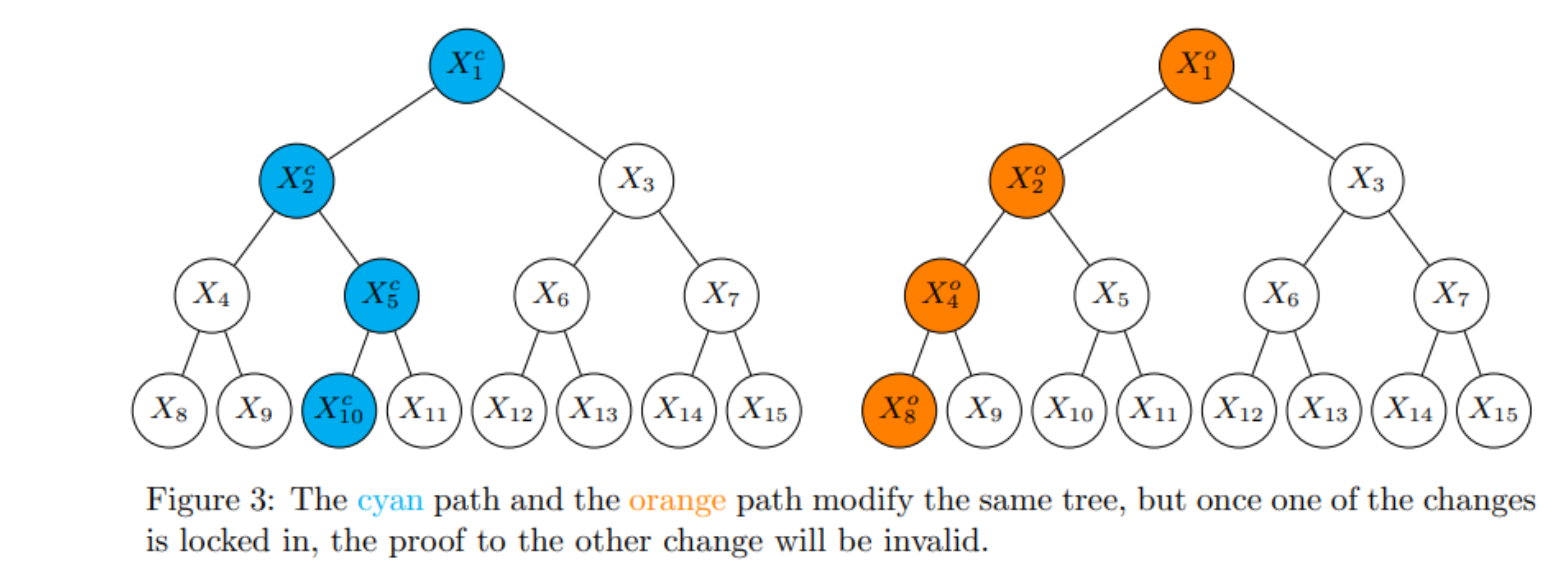
当并发执行更新操作时，传统默克尔树会出现操作失败的问题。

如图，当更新了 $X_{10}^c$ 后，如果同时并发地去更新 $X_8^a$，在更新之前会先验证传入的 proof 是否正确，那么此时就会出现 proof 匹配不上的问题，传入的是 $X_5$ ，但实际 $X_5$ 已经被更新成了 $X_5^c$，而现在的 $X_1^c$ 显然不等于 $H(H(H(X_8,X_9),X_5),X_3)$。

Concurrency Tree

在 Solana 中存在对 Merkle Tree 并发操作的情况，spl-account-compression 是具体的链上实现，而 Concurrency Merkle Tree 实现的代码在这: concurrent-merkle-tree。

其原理是通过在默克尔树结构中外带一个 Changelog 数组来缓存最近数次的修正记录，并试图与当前期望证明的 root 进行匹配，匹配成功后将后续 Changelog 应用于当前期望证明的 proof 和 root 上，从而能够使用目前 active 状态的 root 进行证明。

replace leaf And append

下面解释白皮书中涉及的两个重要操作：replace leaf 和 append，首先解释 replace leaf。

并发默克尔树引入了这样一个 Changelog 结构去存储每次更新的 Path，而这个 Path 又可以由 leaf index 来唯一确定，因为 leaf index 的二进制表示等价于每一层左右子树的走向，比如叶子节点序号 $2(\text{010})$ 在 $D=3$ 的树中路径为左-右-左。 所以每一个 Changelog 只需要记录:

• root: change 发生时计算的 root
• path: 更新的路径，包括 leaf 但不包括 root
• index: 发生更新的 leaf 的序号，主要在哈希的时候奇偶性用来判断左右子节点

当该 Changelog 被应用时，有两种情况

• changelog_index != leaf_index: 显然树上两节点会存在公共 Path 部分，而需要更新的 Proof 即为最近公共祖先的子节点。算法实现的话使用双方的 leaf index 进行异或操作再匹配前导零即为公共路径长度
• changelog_index == leaf_index: 直接替换 leaf 即可

白皮书代码实现 replace leaf

同时并发默克尔树还维护了一个 rightmost proof 用以支持最大叶子节点数的并发 append；思路沿用前面的 replace leaf，同样计算最近公共祖先，然后将 Path 分成三部分：

1. 公共路径部分：显然就是 rightmost proof 上相应的 Path
2. 祖先关键节点：去拿由 rightmost proof 算到当前层的哈希值
3. 其余部分：新叶子在左边位置参与与空值 sibling 的哈希运算结果

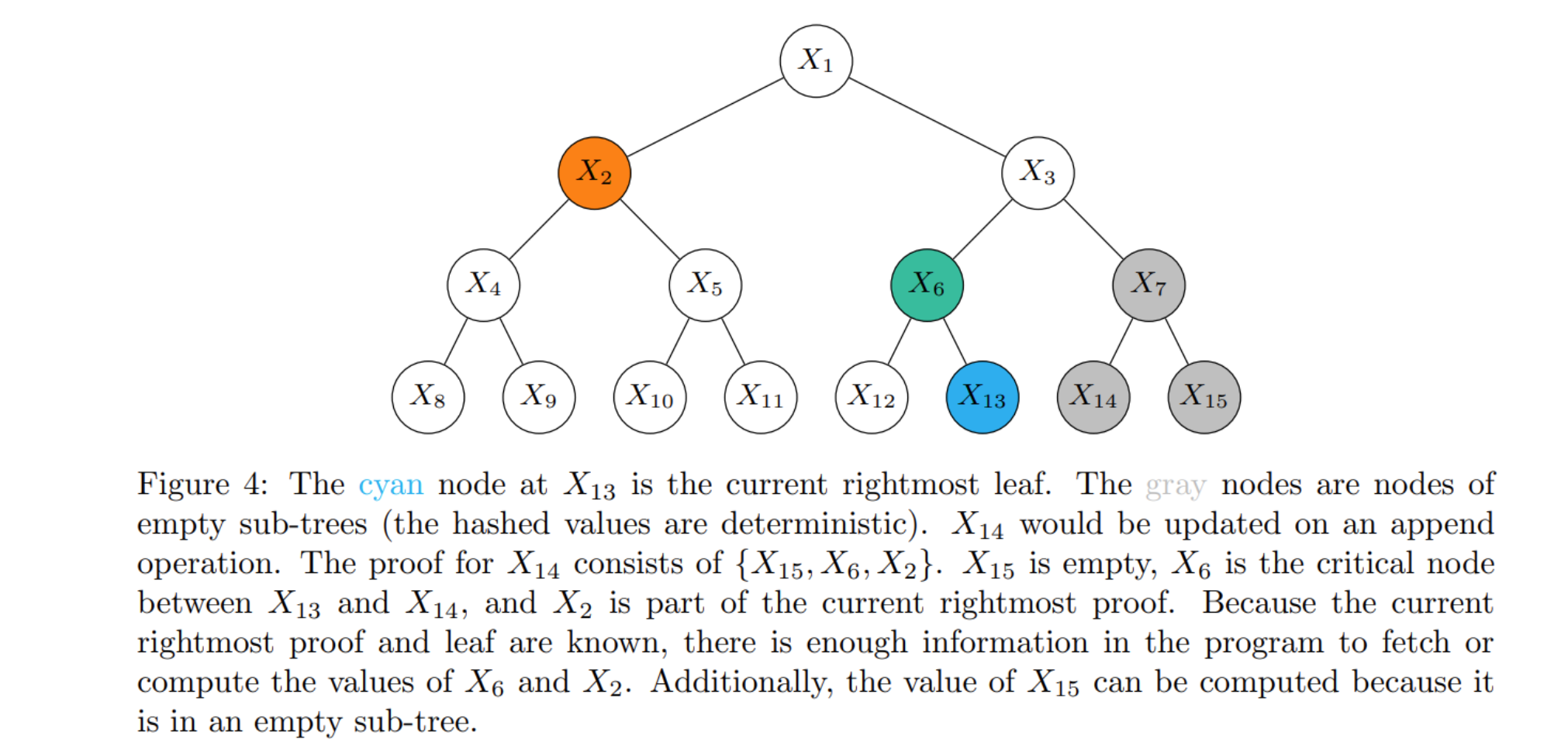
可能文字表述有点抽象可以看看白皮书给的示例图：

现在准备 append 添加 $X_{14}$，需要构造 proof $\{X_{15},X_6,X_2\}$，$X_2$ 的值便是情况 1 直接从 rightmost path 中获取；$X_6$ 是情况 2，通过对 rightmost proof 一直向上计算到这个位置就能获得；$X_{15}$ 是情况 3，由全空叶子节点进行逐级构造。 然后直接看这段代码也挺好理解的：

for (i, cl_item) in change_list.iter_mut().enumerate().take(MAX_DEPTH) {
	*cl_item = node;
	match i {
		i if i < intersection => {
			// Compute proof to the appended node from empty nodes
			let sibling = empty_node_cached::<MAX_DEPTH>(i as u32, &empty_node_cache);
			hash_to_parent(
				&mut intersection_node,
				&self.rightmost_proof.proof[i],
				((self.rightmost_proof.index - 1) >> i) & 1 == 0,
			);  
			hash_to_parent(&mut node, &sibling, true);
			self.rightmost_proof.proof[i] = sibling;
		}
		i if i == intersection => {
			// Compute the where the new node intersects the main tree
			hash_to_parent(&mut node, &intersection_node, false);
			self.rightmost_proof.proof[intersection] = intersection_node;
		}
		_ => {
			// Update the change list path up to the root
			hash_to_parent(
				&mut node,
				&self.rightmost_proof.proof[i],
				((self.rightmost_proof.index - 1) >> i) & 1 == 0,
			);
		}
	}
}

白皮书实现伪代码 append：

Tree in Code

首先是树的结构：

pub struct ConcurrentMerkleTree<const MAX_DEPTH: usize, const MAX_BUFFER_SIZE: usize> {
    pub sequence_number: u64,
    /// Index of most recent root & changes
    pub active_index: u64,
    /// Number of active changes we are tracking
    pub buffer_size: u64,
    /// Proof for respective root
    pub change_logs: [ChangeLog<MAX_DEPTH>; MAX_BUFFER_SIZE],
    pub rightmost_proof: Path<MAX_DEPTH>,
}

• sequence_number 表示当前树的序号，每次对树的数据进行更改操作都会使该值自增1。
• active_index 用来存储最近一次 root change 的记录，使用 self.change_logs[active_index] 获取当前最新的树根 hash，传入的每次 proof 也都需要通过算法应用之前的 Changelog 后来跟这个 root 进行计算证明
• buffer_size 用来表示现在我们保存的 change log 数目，其一直自增直到设置的最大值，这个跟 active_index 搭配可以循环使用 change_logs，example:

for i in 0..self.buffer_size {
	let j = self.active_index.wrapping_sub(i) & mask as u64;
	...
}

初始化

• initialize，用来直接初始化一个树，并让每个叶节点的值都为 [0_u8; 32] 并以此计算 root ($Father=H(child,child)$)，装入 change_logs 中，同时记录 rightmost_proof
• initialize_with_root，跳过这个函数的解释

白皮书中也提及了并发默克尔树的初始化为一颗叶子节点全零的满二叉树。对于空值的哈希运算进行正常处理向上传递：

叶子证明

• prove_leaf: 证明叶子节点在当前树上，传入: 当前 root，叶子节点，proof 路径，叶子节点序号
  • 经过一些检查后来到 check_valid_leaf
  • 查看能否在 changelog 中直接找到 history root，然后进入 fast_forward_proof 中进行 proof 的更新
    • 能找到，那直接从这个历史开始更新使用之后的 ChangeLog 来更新 proof
    • 如果开启 allow_inferred_proof，那么在不能找到的情况下，会遍历整个 buffer 区尝试去构造 proof path 出来
    • 上述两种情况在遍历 change log 时碰见 leaf index 相同时更新 leaf
  • check leaf 是否发生变化，若发生变化意味着出现冲突，直接返回 Error
  • 用 leaf 和 proof path 计算 root 是否符合预期 change_logs[active_index]

这里的处理对应了并发场景的下的几种情景:

1. 传入的 current_root 恰好是 change_logs[active_index]，那就直接用传入的 proof 和 leaf 证明即可
2. 传入的 current_root 不是 change_logs[active_index]，但是能够在 changelog 中找到 history root 与之相等，那么就再将该 history log 之后直到 active_index 的记录应用在传入的 proof 上，最后同样与 change_logs[active_index] 的 root 进行证明
3. 传入的 current_root 在 changelog 中找不到，那么便试图遍历整个 change log 来应用 proof path 和 leaf

添加/更改叶子

这里主要有两个方法，一个是 append:

• 如果是第一次，那么调用 initialize_tree_from_append 方法
• 否则便使用 rightmost_proof 进行 path 的生成

另一个是 fill_empty_or_append，主要用来在指定 index 上加入一个 leaf，但需要满足之前的 leaf 为空:

• check_valid_leaf 先证明当前 index 为空时使用 proof path 以及传入的 root 是否合法
• update_buffers_from_proof 中更新 change_logs 和 rightmost_proof
  • 使用传入的 leaf 和 proof path 计算更新的 path
  • 依据 leaf index 来更新 rightmost_proof
• 如果前述方法失败那么会 fallback 到 append

还有一个 set_leaf 提供对于指定 index 非空叶子节点的更换，跟 fill_empty_or_append 差不多，不同之处在于 set_leaf 只能更换非空叶子节点，fill_empty_or_append 预期是更换空叶子节点，就算失败也会再次尝试 append 方法。

Resolution of Historical Potential Vulnerabilities

1. 部分链实现会在非叶子节点哈希计算之前按左右子节点的大小进行排序，因此传入叶子节点 $L_A,R_B$ 会对 $L_B,R_A$ 造成分叉或双花攻击

Solved: 并发默克尔树不会进行排序，Hash(L+R) 和 Hash(R+L) 结果在 $L\ne R$ 的情况下不一致

2. 部分链实现会对奇数个叶节点后复制一份最后的叶节点，那么构造一个相同的树同样能够造成分叉或双花攻击

Solved: 并发默克尔树是满二叉树，并且不会复制，直接使用空叶节点值参与Hash生成

3. 部分链实现的默克尔树是完全二叉树，传入的 proof 没有 size 限制，因此如果知道树上前 N 层的节点，可以通过传入一个 proof path 上的值当作 fake leaf 和一个很短的 proof 路径从而完成 root 验证

Solved: Solana 的默克尔树是满二叉的，传入 proof 虽然也没有长度限制但是仍会以某种方式填充到固定长度 (树的深度)

SPL Account Compression

这个是链上的交互并发默克尔树实现，相比于前面的树结构外，主要提供了:

• 新增了 canopy 用于缓存树的前 N 层节点，从而减少传入的 proof path 数量
• 新增了 ConcurrentMerkleTreeHeader 用于储存并发默克尔树的信息比如 authority，max_buffer_size，max_depth
• MerkleTree Account 结构：Header + tree data ( + canopy data)
• 链上通过 remainning_account 的 key 来传入 proof

Ref

• 西师傅的探索
• vanish 师傅 starCTF2022 WP
• Concurrent Merkle Tree Whitepaper